Heaps, Priority Queues, and Heapsort

We want to be able to implement priority queues – structures where you can easily get the maximal element.

This should support:

• Creation
• Insertion of element
• Deletion of element
• Nice functionality

Heaps

A heap is a data structure that gives easy access to the most extreme element, or the highest priority element.

Heaps use complete binary trees (not binary search trees!) as the underlying structure, but are often implemented using arrays.

Trees

Remember that a tree is:

• An undirected graph that has no cycles.
• Equivalently, there is a single shortest path from one node to any other node.
• There is a root node
• Ancestor nodes: parent of a parent...
• Descendents: child of a child...
• Internal node: has children
• Leaf node: does not have children

We say:

The depth of a root node is 0, and the depth of a node is the depth of its parent plus one.

The height of a leaf is 0, and the height of a node is the height of its child + 1.

The max height or depth of a node is the maximum of its nodes.

Binary Trees

The number of children per node is at most two. This means that the degree of each node is 3 or less.

Complete binary tree: A binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Implementation

template <class Item>
struct Node {
    Item item;
    Node *left;
    Node *right;
};

• A node contains some information, and has a left and right child node. You can also include a pointer to its parent.
• You could also use an array and indices instead of pointers.

Heap-Ordered Trees, Heaps

A heap is a binary tree with the property that a parent node is at least as large as both of its children. This means that the tree is (max)-heap-ordered.

Finding Children and Parents

To find the key of a child, the child keys are at indices key, and key + 1. To find the parent of a key, divide the child key by 2 (using floor division).

Array-based Heaps

• You need a number of data items MAX_HEAP.
• You need data members items, a list of items, and size, an integer representing the size.

Breaking and Fixing

Bottom-up heapify

Let's say you take one of the elements in the heap, and you suddenly increase the value of it. How do you fix it so that it still supports the max heap condition?

You just successively move the element up the tree until it is at the correct position, or until it is at the root of the tree!

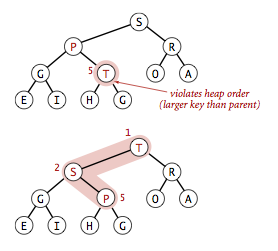
Here is some pseudocode:

void fixUp(Item heap[], int k) {
    while (k > 1                  // Item is not root
        && heap[k/2] < heap[k]) { // while parent is less than child
        swap(heap[k], heap[k/2];
        k /= 2; // move up
    }
}

Top-down heapify

Let's say you take one of the elements in the heap, and you suddenly decrease its value. How do you fix the max heap condition?

You swap the given node with the largest child key, until you:

• reach the bottom of the heap
• no children have a larger key

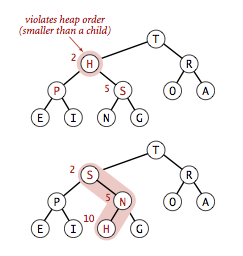
Here is some pseudocode:

void fixDown(Item heap[], int heapsize, int k) {
    while (2 * k <= heapsize) {
        int j = 2 * k; // index of left child
        if (j < heapsize && heap[j] < heap[j + 1]) j++;
        if (heap[k] >= heap[j]) break;
        swap(heap[k], heap[j]);
        k = j;
    }
}

Priority Queue

A priority queue is a data structure that supports two basic operations:

• Insertion of a new item: enqueue()
• Removal of the item with the largest key: dequeue()

Priority queues are essential for shortest path algorithms. They are useful for some algorithms like heapsort, sorting in reverse order.

Priority queues are often implemented using heaps because insertion/removal operations are the same.

Insertion

Insertion can really just be viewed as just an operation where you append the item to the end of the array, and you use the fix up operation!

void insert(Item newItem) {
    heap[++N] = newItem;
    fixUp(heap, N);
}

The complexity of this is \(O(\log n)\), since that is the complexity of the fix operations.

Deletion

Deletion operation can only remove the root, and must maintain the heap invariants.

You remove the root element, move the last element into the root position, and the new root "trickles down" using fixDown()!

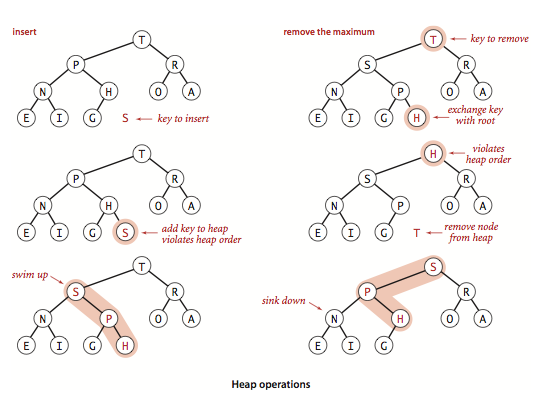
Building a Heap (Heapify)

Given an array, how could you create a heap out of it?

You could just view a heap building as an insertion of \(n\) elements into the heap, each in \(\log n\) time (hence \(O(n \log n)\) time). This also requires an extra array to store the new heap in. This is kind of inefficient.

Instead, just take the given array, and perform repeated fixDown() operations proceeding from bottom to top. This has \(O(n)\) time with an ugly proof.

Heapsort

This is known as heapsort. You repeatedly dequeue the highest priority item from a priority queue.

void heapsort(Item heap[], int n) {
    buildHeap(heap, n);
    for (int i = n; i >= 2; --i) {
        swap(heap[i], heap[1]); // swap with root
        fixDown(heap, i - 1, 1);
    }
}

Take the given \(n\) elements, and convert into a heap using heapify in \(O(n)\) time. Remove the elements one at a time, filling the original array from back to front in \(O(n \log n)\) time. Hence, the total runtime is \(O(n \log n)\) time and requires no additional space.

Summary

In summary:

• Priority queues are an ADT that supports insertion and removal of the maximal element.
• An unordered array allows for the \(O(1)\) insertion of an item, and the \(O(n)\) removal of the largest item.
• A heap allows for efficient \(O(\log n)\) insertion and removal of the largest and smallest items
  • Operations must be able to maintain the heap property – fixUp() and fixDown() must not violate the heap condition
• Heapsort
  • \O(n \log n\) sort that takes advantage of heap properties.